HISTORIA DE LOS SISTEMAS DE ECUACIONES Los sistemas de ecuaciones eran ya resueltos por los babilonios los cuales llamaban a las incógnitas con palabras como longitud, anchura, o volumen sin que tuvieran relación con problemas de medida.
Los griegos también resolvían algunos sistemas de ecuaciones pero utilizando métodos geométricos. También aparecen en los documentos hindúes y chinos la aplicación de sistemas de ecuaciones.
CONCEPTO
Un sistema de ecuaciones es la reunión de dos o más ecuaciones que deben satisfacerse para los mismos valores de las incógnitas o variables.
Para indicar que varias ecuaciones forman un sistema, se abarca el conjunto de todas ellas con una llave.
Para indicar que varias ecuaciones forman un sistema, se abarca el conjunto de todas ellas con una llave.
Así, se puede encontrar sistemas con dos o mas incógnitas que son resueltos por métodos ya conocidos.
TIPOS DE SISTEMAS DE ECUACIONES
Los sistemas de ecuaciones se pueden clasificar según el número de soluciones que pueden presentar. De acuerdo con ese caso se pueden presentar los siguientes casos:
Sistema compatible si tiene solución, en este caso además puede distinguirse entre:
- Sistema compatible determinado cuando tiene una única solución. Gráficamente las rectas se cortan en un único punto.
- Sistema compatible indeterminado cuando admite un conjunto infinito de soluciones. Gráficamente la solución se encuentra sobre la recta en infinidad de puntos.
Sistema incompatible si no tiene solución. Gráficamente las rectas son paralelas, entonces no tienen punto común de intersección.
En el caso de los sistemas 3x3 las soluciones pueden ser:
MÉTODOS PARA LA SOLUCIÓN DE SISTEMAS DE ECUACIONES LINEALES
Método de Sustitución
El método de sustitución consiste en despejar en una de las ecuaciones cualquier incógnita, preferiblemente la que tenga menor coeficiente, para, a continuación, sustituirla en otra ecuación por su valor.
REGLA: Para la eliminación por Sustitución, se siguen los siguientes:
1. Se despeja una de las incógnitas de una de
las ecuaciones del sistema.
2. Se sustituye este valor obtenido en la otra
ecuación.
3. Se resuelve la ecuación de primer grado con
una incógnita que así se obtiene.
4. El valor obtenido se sustituye en cualquiera
de las ecuaciones originales.
5. Se comprueba la solución, sustituyendo los
valores obtenidos en las ecuaciones dadas.
En caso de sistemas con más de dos incógnitas, la seleccionada debe ser sustituida por su valor equivalente en todas las ecuaciones excepto en la que se ha despejado. En ese instante, se tendrá un sistema con una ecuación y una incógnita menos que el inicial, en el que se puede seguir aplicando este método reiteradamente.
Método de igualación
El método de igualación se puede entender como un caso particular del método de sustitución en el que se despeja la misma incógnita en dos ecuaciones y a continuación se igualan entre sí la parte derecha de ambas ecuaciones, posteriormente se reemplaza el valor de la variable encontrada en una de las ecuaciones despejadas.
Una vez encontrados los valores de las variables o incógnitas se procede a la verificación de la solución del sistema.
Método de reducción
Este método suele emplearse mayoritariamente en los sistemas lineales, siendo pocos los casos en que se utiliza para resolver sistemas no lineales. El procedimiento, diseñado para sistemas con dos ecuaciones e incógnitas, consiste en transformar una de las ecuaciones (generalmente, mediante productos), de manera que obtengamos dos ecuaciones en la que una misma incógnita aparezca con el mismo coeficiente y distinto signo.
A continuación, se suman ambas ecuaciones produciéndose así la reducción o cancelación de dicha incógnita, obteniendo así una ecuación con una sola incógnita, donde el método de resolución es simple. Por ejemplo:
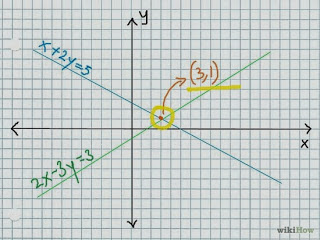
Método Gráfico
Consiste en construir la gráfica de cada una de las ecuaciones del sistema. El método (manualmente aplicado) solo resulta eficiente en el plano cartesiano, es decir para un espacio de dimensión 2.
El proceso de resolución de un sistema de ecuaciones mediante el método gráfico se resuelve en los siguientes pasos:
1. Se despeja la incógnita (y) en ambas ecuaciones. Se construye para cada una de las dos ecuaciones de primer grado obteniendo la tabla de valores correspondientes.
2. Se representan gráficamente ambas rectas en los ejes coordenados.
3. En éste último paso hay tres posibilidades planteadas en las solución de ecuaciones:
a) Si ambas rectas se cortan, las coordenadas del punto de corte son los únicos valores de las incógnitas (x,y). "Sistema compatible determinado".
b) Si ambas rectas son coincidentes, el sistema tiene infinitas soluciones que son las respectivas coordenadas de todos los puntos de esa recta en la que coinciden ambas. «Sistema compatible indeterminado».
c) Si ambas rectas son paralelas, el sistema no tiene solución en los reales pero si en los complejos.
APLICACIÓN DE LOS SISTEMAS DE ECUACIONES
Son muchas las áreas donde se utilizan los sistemas de ecuaciones a diario, la gente tiende a no pensar en términos de ecuaciones y fórmulas en sus vidas diarias. Usan el lenguaje para describir la situación.
Pero las palabras se pueden traducir en el lenguaje de las matemáticas. Tomemos un ejemplo muy simple: una madre tiene que dividir seis manzanas entre tres hijos. Sin esfuerzo se llega a la conclusión de que cada niño recibe dos manzanas. Lo que se ha utilizado es la función matemática de la división para llegar a la respuesta: 6/3 = 2.así:
Calcular tiempos de viaje
Supongamos que tu oficina se encuentra a 30 kilómetros de tu casa. Tienes que llegar a las 8 de la mañana, y sabemos que el tráfico se mueve a 60 millas por hora. Para saber la hora exacta en la que debes salir de casa, traduce la palabra problema en una ecuación: tiempo total = distancia dividida entre la velocidad de desplazamiento.
Así que t (tiempo) = D (distancia) / r (tasa), y T = 30/60. Así que t = 1/2 o media hora. Para llegar a la oficina a las 8 de la mañana, debe salir a las 7:30 de la mañana.
Convertir de horas a minutos
¿Cuántos minutos hay en cuatro horas? Sea x = el número de horas, y = el número de minutos. Por definición, hay 60 minutos en una hora. Así que puedes escribir una ecuación para describir esta relación: y = 60x. El número de minutos es igual a 60 veces el número de horas. Por ejemplo, supongamos que x = 4. A continuación, conecta el número en la ecuación lineal para obtener y = 60 * 4. Por lo tanto y = 240 minutos.
Pesos y medidas
Digamos que tu receta requiere de 100 gramos de harina, pero sólo se puede llegar a pesar en onzas. Se utiliza una fórmula matemática para convertir de gramos a onzas. O bien, medir el camino de entrada para calcular la cantidad de cemento que tendrá que preparar. Presupuesto, inversión, costura, cocina - las matemáticas están en todas partes.
BIBLIOGRAFÍA:
- Matemática 4, Editorial Don Bosco
- Matemática 4, Editorial La Hoguera
http://www.ehowenespanol.com/ecuaciones-lineales-dia-dia-hechos_39447/
No hay comentarios:
Publicar un comentario